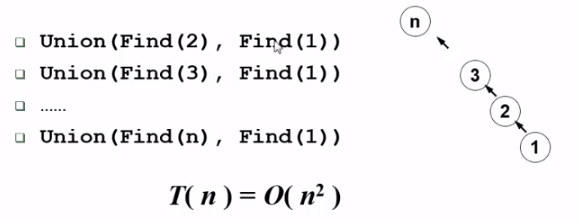DS浙大

第一周

1-2-2

递归的空间复杂度很大：

而循环通常只对一块内存反复使用。

计算机计算乘除法会比加减法慢很多。所以乘法越多，时间复杂度越大。

1-2-3

Ω表示复杂度上界

O表示复杂度下界

Θ表示上下界一致

具体如下：

第二周

课后练习 一元多项式的乘法与加法运算

函数题:02-线性结构1 两个有序链表序列的合并

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
    ElementType Data;
    PtrToNode   Next;
};
typedef PtrToNode List;

List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表；空链表将输出NULL */

List Merge( List L1, List L2 );

int main()
{
    List L1, L2, L;
    L1 = Read();
    L2 = Read();
    L = Merge(L1, L2);
    Print(L);
    Print(L1);
    Print(L2);
    return 0;
}

/* 你的代码将被嵌在这里 */

分析题目

题目的关键：直接使用原序列中的结点。

代码

List Merge(List L1,List L2){
    List Head,t1,t2;
    List L=(List)malloc(sizeof(List));
    L->Next=NULL;
    Head=L;

    t1=L1->Next;
    t2=L2->Next;

    while(t1 && t2){
        if(t1->Data <= t2->Data){
            L->Next=t1;
            L=t1;
            t1=t1->Next;           
        } else if(t2->Data < t1->Data){
            L->Next=t2;
            L=t2;
            t2=t2->Next;
        }
    }
    
    L->Next= t1 ? t1:t2;// (1)
    L1->Next=NULL;      // (2)
    L2->Next=NULL;
    return Head;
}

(1)可以用来代替

if(t1)
	L->next=t1;
else
	L->next=t2;

用来挂上剩余的链表。

（2）题目要求在原来的链表上操作，因此完成后需要把L1和L2设置为空链表。

第三周 树(上)

树的问题本质上是通过递归的方式简化为“根左右”的方式来处理。

一棵树想用顺序存储结构来表示显然是不方便的，因此我们通常用链式存储结构来表示。

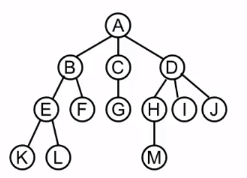
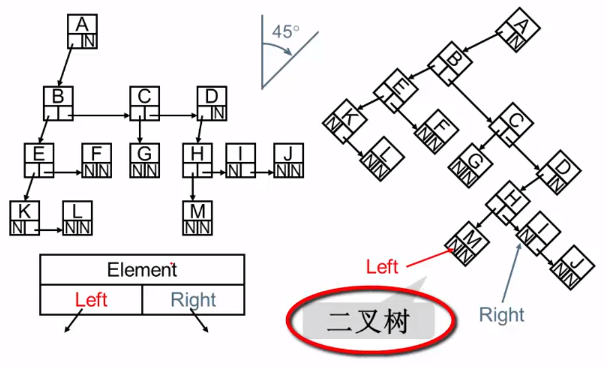
对于这棵树，优先能想到的链式表示方法如下：

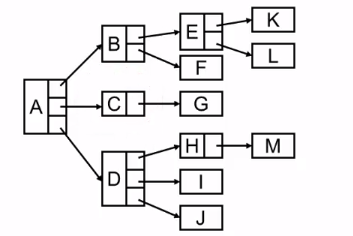
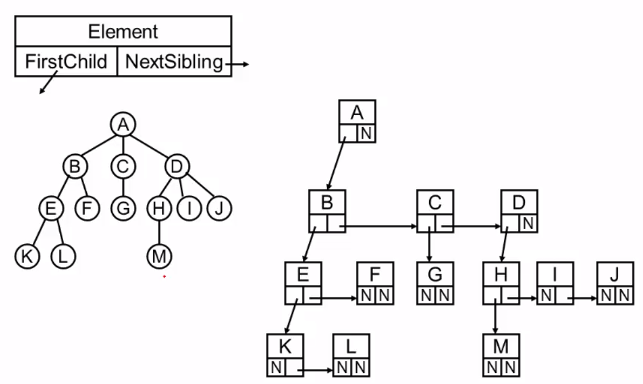
这种方法有个缺陷，需要定义多种不同类型的结构体，非常不方便。如果我们把所有结点设计成度最大的结构，对于指针域又是一种极大浪费，因此就引入了孩子兄弟表示法。如图所示：

这样只会浪费n+1个指针域，也统一了结点的样式，而右边这个样式，就是二叉树。

二叉树

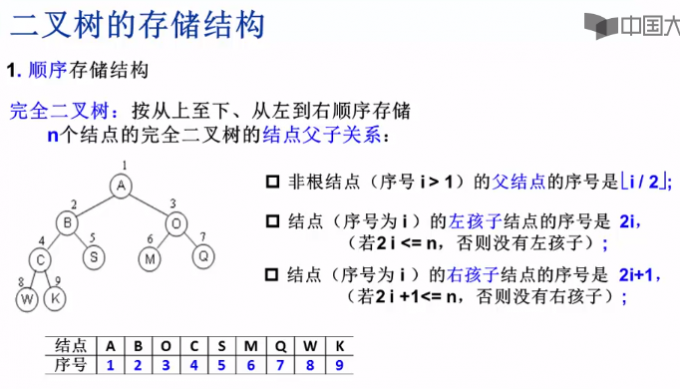
二叉树是可以进行顺序存储的

完全二叉树很适合顺序存储

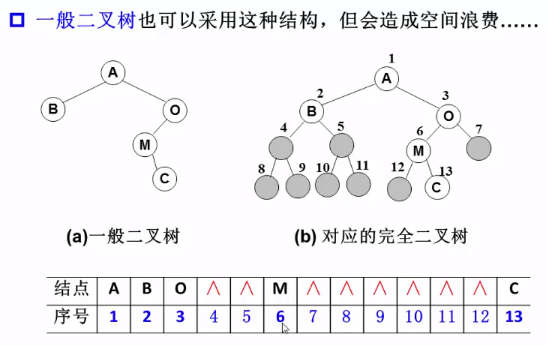
非完全二叉树也可以顺序存储，只要将其补成完全二叉树即可，但会浪费很多空间：

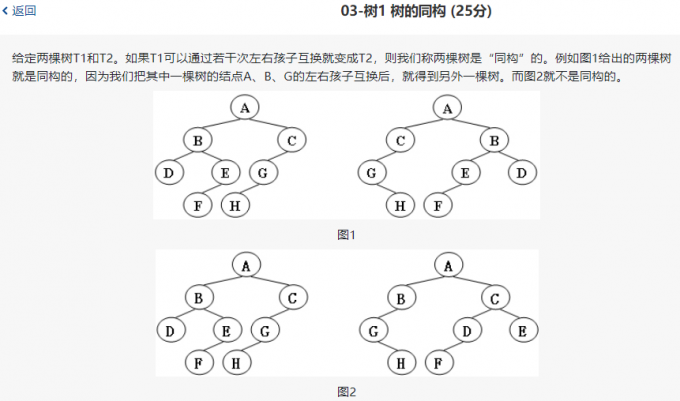
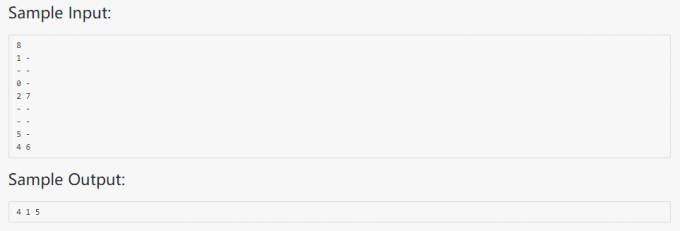
03-树1 树的同构

#define Tree int
#define MaxSize 10
#define Null -1
#include <stdio.h>

struct Node{
    char data;
    Tree left;
    Tree right;
}T1[MaxSize],T2[MaxSize];
typedef struct Node treeNode;

Tree BuildTree(treeNode T[]);
Tree isomorphic(Tree R1,Tree R2);

int main()
{
    Tree R1,R2;

    R1=BuildTree(T1);
    R2=BuildTree(T2);
    if(isomorphic(R1,R2)) printf("Yes\n");
    else printf("No\n");
}
Tree BuildTree(treeNode T[]){
    Tree n,root=Null;//如果是空树返回null
    char cl,cr;
    scanf("%d",&n);
    getchar();
    Tree check[n];

    if(n){

        for(int i=0;i<n;i++)
            check[i]=0;

        //顺序存储二叉树
        for(int i =0;i<n;i++){
            scanf("%c %c %c",&T[i].data,&cl,&cr);    // (1)
            getchar();
            if(cl!='-')
                T[i].left=cl-'0';
            else
                T[i].left=Null;
            if(cr!='-')
                T[i].right=cr-'0';
            else
                T[i].right=Null;

        }


        //left和right中没出现过的序号就是根节点
        for(int i=0;i<n;i++){
            if(T[i].left>=0)
                check[T[i].left]=1;
            if(T[i].right>=0)
                check[T[i].right]=1;
        }
        //找到根结点并返回
        for(int i=0;i<n;i++){
            if(!check[i])
                root=i;
        }
    }
    return root;
}

Tree isomorphic(Tree R1,Tree R2){
    if((R1==Null)&&(R2==Null))//both empty
        return 1;
    if( (R1==Null) && (R2!=Null) || (R1!=Null) && (R2==Null) )//one of them is empty
        return 0;
    if( T1[R1].data!=T2[R2].data ) //roots are different
        return 0;
    if( (T1[R1].left==Null) && (T2[R2].left==Null) ) //both have no left subtree
        return isomorphic(T1[R1].right,T2[R2].right);
    if( ( (T1[R1].left!=Null) && (T2[R2].left!=Null) ) && (T1[T1[R1].left].data)==(T2[T2[R2].left].data) )
        return (isomorphic(T1[R1].left,T2[R2].left) &&
                isomorphic(T1[R1].right,T2[R2].right));
    else return (isomorphic(T1[R1].left,T2[R2].right) &&
                 isomorphic(T1[R1].right,T2[R2].left));

}

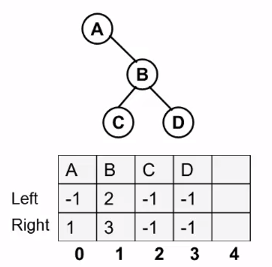
（0）用静态链表来做这题，即下面例子中的存储格式：

（1）scanf()中如果带有\n，那么只有当它遭遇到下一个非空格字符时才会执行。

Using “\n” in scanf() in C

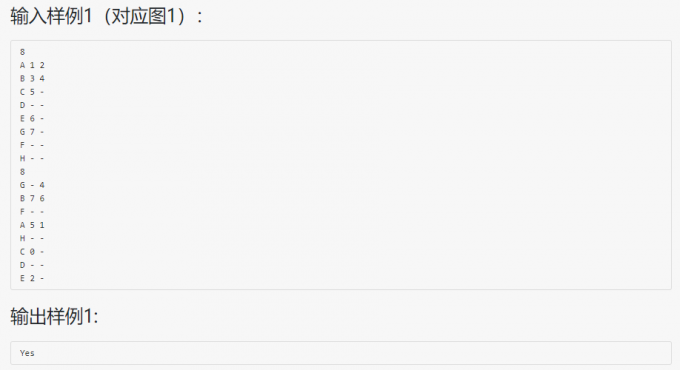
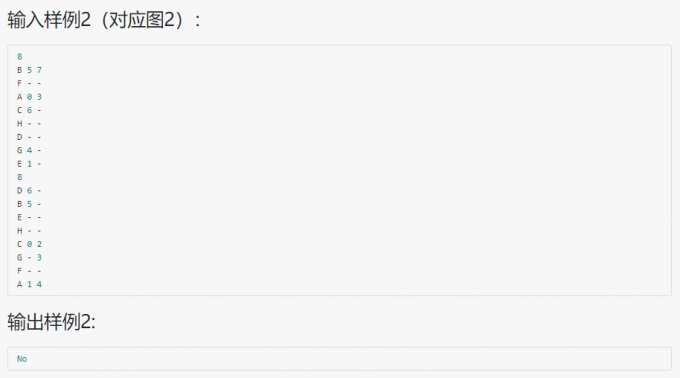
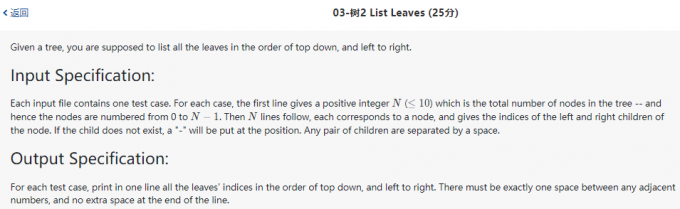
03-树2 List Leaves

代码：

#define Tree int
#define MaxSize 10
#define Null -1
#include <stdio.h>

struct Node{
    Tree length;
    Tree data;
    Tree left;
    Tree right;
}T1[MaxSize],queue[MaxSize];
typedef struct Node treeNode;


Tree BuildTree(treeNode T[]);
void searchLeaf(Tree R);

int main()
{
    //建立一棵树
    Tree R1;
    //R1代表根节点下标
    R1=BuildTree(T1);
    //输出叶子结点
    searchLeaf(R1);
    //printf("%d",R1);
}


void searchLeaf(Tree R){
    int i=0;
    Tree front=0,rear=0;
    treeNode tempNode;

    if(R>=0){
    /******层次遍历********/

        //根节点入队
        queue[rear]=T1[R];//结构体数组元素可以直接赋值吗？
        rear++;

        while(front<T1[R].length){
            //节点出队
            tempNode=queue[front];     //(2)
            front++;
            //每次扫描到一个节点就判断是否为叶子节点
            if( (tempNode.left==Null) && (tempNode.right==Null) ){
                printf(i==0 ? "%d":" %d",tempNode.data);
                i++;
            }
            if(tempNode.left!=Null){
                //将节点的孩子节点入队
                queue[rear]=T1[tempNode.left];
                rear++;
            }
            if(tempNode.right!=Null){
                queue[rear]=T1[tempNode.right];
                rear++;
            }
        }
    }
    else
        //树为空的情况
        printf("Null\n");
}

Tree BuildTree(treeNode T[]){
    Tree N,root=Null;
    char cl,cr;
    scanf("%d",&N);
    getchar();
    Tree check[N];
    for(int i=0;i<N;i++) check[i]=0;

    if(N){
        for(int i=0;i<N;i++){
            scanf("%c %c",&cl,&cr);
            getchar();
            T[i].data=i;
            T[i].length=N;
            if(cl!='-'){
                T[i].left=cl-'0';
                check[T[i].left]=1;
            }
            else T[i].left=Null;
            if(cr!='-'){
                T[i].right=cr-'0';
                check[T[i].right]=1;
            }
            else T[i].right=Null;
        }
        for(int i=0;i<N;i++){
            if(!check[i]){
                root=i;
                break;
            }
        }
    }

    return root;
}

(1)层序遍历需要用到队列，为了方便我直接用了顺序存储的队列。

(2)一般来说，结构体变量可以用另一个变量对其进行赋值和初始化，但是成员中含有指针时上面的情况就无法实现。

C语言中结构体直接赋值？

第四周 树(中)

二叉搜索树

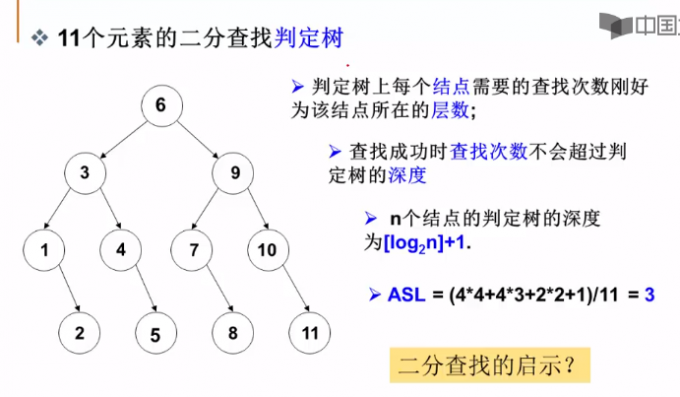
查找分为静态查找和动态查找（查找过程中需要插入，删除等操作）。我们知道二分查找可以提高查找效率，是因为其查找过程可以建立为一棵树，因此我们不如直接将数据的形式按照树的方式存储，这样还可以进行动态查找，这棵树就叫二叉搜索树。

如何建立一棵二叉搜索树：

TreeNode makeTree(int n){
    //建立一棵二叉搜索树    
    TreeNode T;
    int V;


    scanf("%d",&V);//读入第一个节点
    T=newNode(V);//建立根节点  (1)
    for(int i=1;i<n;i++){
        scanf("%d",&V);
        //插入新节点
        T=insertNode(T,V);
    }
    return T;
}

//新建节点
TreeNode newNode(int v){
     TreeNode T=malloc(sizeof(TreeNode));
     T->data=v;
     T->left=NULL;
     T->right=NULL;
     T->flag=0;
     return T;
}

//插入节点建立二叉搜索树
TreeNode insertNode(TreeNode T,int v){
    if(!T) T=newNode(V); //
    else{
        if(V>T->data)
            T->right=insertNode(T->right,V);
        else
            T->left=insertNode(T->left,V);
    }
    return T;

}

关于建树的一些小tip：

(1) 先建立根节点，再读入，这样才能把根节点记录下来

(2)建树的过程大致为：先建立节点，再插入树中。

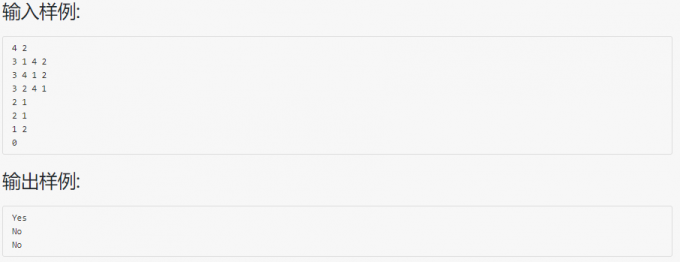
04-树4 是否同一棵二叉搜索树 (25分)

代码：

#include<stdio.h>
#include<stdlib.h>

//构造出一个节点
typedef struct TreeNode{
    int data;
    struct TreeNode *left;
    struct TreeNode *right;
    int flag;//标记节点是否被访问过，用来判断系列是否一致
}TreeNode;

TreeNode* makeTree(int n);
TreeNode* newNode(int v);
TreeNode* insertNode(TreeNode *T,int v);
int judge(TreeNode *T,int N);
int check(TreeNode *T,int V);
void resetTree(TreeNode *T);
void freeTree(TreeNode *T);

int main()
{
    int N,L;
    TreeNode *T;
    //每个序列插入N个元素
    //读入N=0时退出
    scanf("%d",&N);
    while(N){
        //对比序列个数L
        scanf("%d",&L);
        //建立第一棵树
        T=makeTree(N);

        //读入测试序列
        for(int i=0;i<L;i++){
            if(judge(T,N)) printf("Yes\n");
            else printf("No\n");
            resetTree(T);   //清除tag，下个序列进行比较
        }
        freeTree(T);    //这组测试结束，释放当前建立的基准树，为下一组数据做准备

        scanf("%d",&N);

    }
    return 0;
}

void resetTree(TreeNode *T){
    if(T){
        resetTree(T->left);
        resetTree(T->right);
        T->flag=0;
    }
}

void freeTree(TreeNode *T){
    if(T){
        freeTree(T->left);
        freeTree(T->right);
        free(T);
    }
}

int judge(TreeNode *T,int N){
    //读入N个序列
    int V=0,flag=0;
    for(int i=0;i<N;i++){
        scanf("%d",&V);//读入一个节点
        if( !check(T,V) ) flag=1;//和树做比较
    }
    if(flag) return 0;
    else return 1;
}

int check(TreeNode *T,int V){
    //当前节点访问过
    if(T->flag){
        if(V>T->data) return check(T->right,V);
        else if (V<T->data) return check(T->left,V);//对比序列个数L
        else return 0;//序列中两个节点相等，则认与二叉树不一致
    } else {
        if(V==T->data){
            T->flag=1;
            return 1;
        }
        else return 0;
    }
}

TreeNode* makeTree(int n){
    //建立一棵二叉搜索树    (1)
    TreeNode *T;
    int V;


    scanf("%d",&V);//读入第一个节点
    T=newNode(V);//建立根节点
    for(int i=1;i<n;i++){
        scanf("%d",&V);
        //插入新节点
        T=insertNode(T,V);
    }
    return T;
}

TreeNode* newNode(int V){
     TreeNode *T=malloc(sizeof(TreeNode));
     T->data=V;
     T->left=NULL;
     T->right=NULL;
     T->flag=0;
     return T;
}

TreeNode* insertNode(TreeNode *T,int V){
    if(!T) T=newNode(V);
    else{
        if(V>T->data)
            T->right=insertNode(T->right,V);
        else
            T->left=insertNode(T->left,V);
    }
    return T;

}

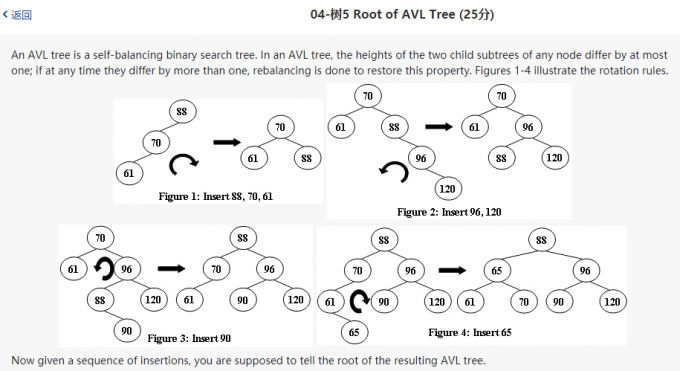
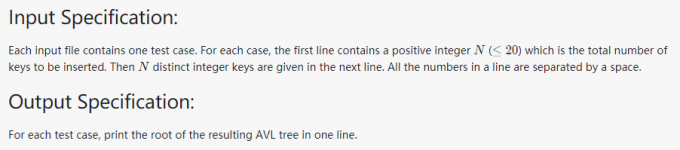
04-树5 Root of AVL Tree (25分)

代码：

#include<stdio.h>
#include<stdlib.h>

//构造出一个节点
typedef struct TreeNode{
    int data;
    int height;
    struct TreeNode *left;
    struct TreeNode *right;
}TreeNode;

TreeNode *createTree(int N);
TreeNode *newNode(int V);
TreeNode *LLRotation(TreeNode *A);
TreeNode *RRRotation(TreeNode *A);
TreeNode *LRRotation(TreeNode *A);
TreeNode *RLRotation(TreeNode *A);
TreeNode *insertNode(TreeNode *T,int V);
int Max(int a,int b);
int getHeight(TreeNode *T);

int main()
{
    int N=0;
    TreeNode *T;
    scanf("%d",&N);
    T=createTree(N);
    printf("%d",T->data);
    return 0;
}

TreeNode *createTree(int N){
    int V=0;
    //T为根节点
    TreeNode *T=NULL;

    for(int i=0;i<N;i++){
        scanf("%d",&V);
        //节点插入树中
        T=insertNode(T,V);
    }
    return T;
}

TreeNode *newNode(int V){
    TreeNode *T=malloc(sizeof(TreeNode));
    T->data=V;
    //这里的高度是从0开始算起，有些书是从1开始
    T->height=0;
    T->left=NULL;
    T->right=NULL;
    return T;
}


TreeNode *insertNode(TreeNode *T,int V){
    //怎么找到需要计算平衡因子的节点  (2)递归思想
    if(!T) T=newNode(V);
    else if(T->data>V){
        T->left=insertNode(T->left,V);
        /* 比较左右子树的高度 */

        /*
        代码中可以看出找到需要调整的子树的方法：
        1、插入一个结点后，从叶子回溯至根结点。
        2、最近的平衡因子=2的结点到插入的叶子结点，其路径上的某三个结点就是需要调整的结点（不一			定包括叶子结点）
        */
        if(getHeight(T->left)-getHeight(T->right)==2){
            if(V<T->left->data) //LL单旋
                T=LLRotation(T);
            else if(V>T->left->data)
                T=LRRotation(T); //LR双旋
        }
    }
    else if(T->data<V){
        T->right=insertNode(T->right,V);
        if(getHeight(T->right)-getHeight(T->left)==2){
            if(V>T->right->data) //RR单旋
                T=RRRotation(T);
            else if(V<T->right->data)
                T=RLRotation(T); //RL双旋
        }
    }
    T->height=Max(getHeight(T->left),getHeight(T->right))+1;
    return T;
}

TreeNode *LLRotation(TreeNode *A){
   /*

            A
           /
          B
         / \
        C   D

   */
    TreeNode *B=A->left;
    A->left=B->right;  //把D挂到A的左子树上
    B->right=A;        //把A挂到B的右子树上
    A->height=Max(getHeight(A->left),getHeight(A->right))+1;//结点高度=max(左右子树的高度)+1
    B->height=Max(getHeight(B->left),A->height)+1;
    return B;

    /*

            B
           / \
          C   A
             /
            D

    */
}

TreeNode *RRRotation(TreeNode *A){
    /*

            A
             \
              B
             / \
            D   C

     */
     TreeNode *B=A->right;
     A->right=B->left;
     B->left=A;
     A->height=Max(getHeight(A->left),getHeight(A->right))+1;
     B->height=Max(getHeight(B->right),A->height);

     return B;

     /*

            B
           / \
          A   C
           \
            D
     */
}

TreeNode *LRRotation(TreeNode *A){
    /*

            A
           /
          B
           \
            C
           /
          D
    LR型，三个结点关系：B<C<A
    所以要把C调整为根节点
    */

    //先以B为根结点RR
    A->left=RRRotation(A->left);

    //再以A为根结点LL
    return LLRotation(A);

    /*

            C
           / \
          B   A
           \
            D
    */
}

TreeNode *RLRotation(TreeNode *A){
    /*

            A
             \
              B
             /
            C
             \
              D
    */

    //对B先做LL旋转
    A->right=LLRotation(A->right);

    //对A做RR旋转
    return RRRotation(A);
    /*

            C
           / \
          A   B
             /
             D

    */
}

int Max(int a,int b){
    return a>=b?a:b;
}

//如何获得左右子树的孩子节点
int getHeight(TreeNode *T){
    return T==NULL?-1:T->height;
}

AVL树的关键：

1、判断失衡的类型(LL、RR、LR、RL)

插入新结点后，找到失衡结点，从失衡结点开始到新结点的路径中数3个结点，他们所构成的就是失衡类型（需要调整的结点并不一定包括新插入结点）

2、LL、RR、LR、RL调整方法

见注释

第五周 树(下)

堆(heap)

如果我们需要一个队列，按照优先级而不是FIFO的形式出队，有下面几种构造方法：

我们发现无论使用那种结构，时间复杂度都为O(n)，但如果使用二叉树的方法，可以大大降低时间复杂度。这种二叉树结构称之为“堆”。

在二叉搜索树中，我们知道搜索树的时间复杂度和树的高度有关，因此我们可以用完全二叉树来保持堆的左右子树的平衡，而为了方便删除最大优先级(或最小，以下都以最大为例)结点，我们把优先级最大的结点记为根结点。

因此，堆的两个条件：

• 完全二叉树
• 任一子树，其根结点优先级都大于其所有孩子结点

因此自顶向下沿着任一路径，结点优先级都是从大到小，我们称为大顶堆（根节点优先级最小，称为小顶堆）。

堆的插入与删除

以最大堆为例，树中元素顺序存储。

• 插入

  完全二叉树在最后插入元素，同自己的父结点比较，若大于父节点，则和父节点交换。

• 删除

  删除堆的根节点元素，用最后一个元素代替，然后与左右孩子结点比较，将其中值最大的移动到根节点。

05-树7 堆中的路径

代码：

#include<stdio.h>
#include<stdlib.h>
#define MAXN 1001
#define MINH -10001

int H[MAXN],size;

void createHeap();
void printHeap();
void insertHeap(int i);

int main(){
    int N=0,M=0; //N为插入元素个数;M为路径条数;
    scanf("%d%d",&N,&M);
    createHeap();
    for(int i=1;i<N+1;i++){
        insertHeap(i);
    }
    for(int i=0;i<M;i++){
        printHeap();
    }

}

void printHeap(){
    int node=0,flag=0;
    scanf("%d",&node);
    for(;node>0;node/=2){
        printf(flag==0?"%d":" %d",H[node]);
        flag=1;
    }
    printf("\n");
}
void insertHeap(int i){
    //建堆
    int temp=0;
    /* 每插入一个元素，和父节点比较，小于父节点则交换 */
    scanf("%d",&H[i]);
    //和父节点比较
    for(;i>0;i/=2){
        if(H[i]<H[i/2]){
            temp=H[i/2];
            H[i/2]=H[i];
            H[i]=temp;
        }
    }

}

void createHeap(){
    H[0]=MINH;
    size=0;//设置哨兵
}

官方参考代码：

插入结点（建堆）：

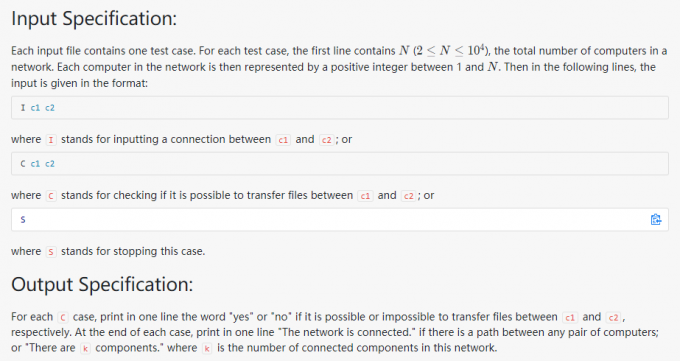
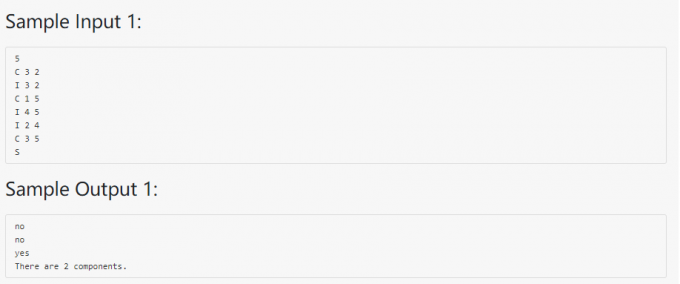
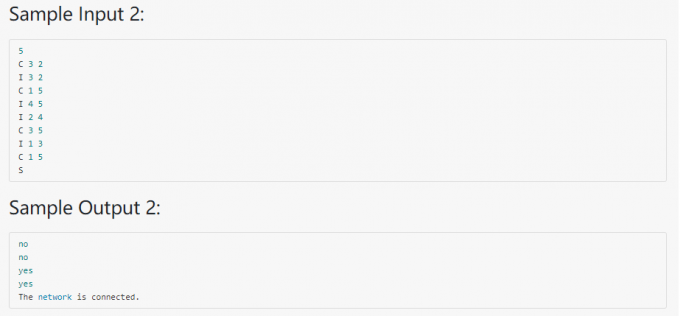
05-树8 File Transfer

代码：

#include<stdio.h>
#include<stdlib.h>

typedef int Setname;
typedef int ElementType;
typedef ElementType SetType;/*定义一个elementType数组类型*/

void initializeUFS(SetType S[],int N);
void checkUnion(SetType S[]);
ElementType Find(SetType S[],ElementType node);
void inputUnion(SetType S[]);
void Union(SetType S[],ElementType root1,ElementType root2);
void searchUnion(SetType S[],int N);

int main(){
    int N=0;
    char in;
    scanf("%d",&N);
    SetType S[N];
    //初始化
    initializeUFS(S,N);

    do{
        scanf("%c",&in);
        switch(in){
            //检查
            case 'C':
                checkUnion(S);
                break;
            //连接
            case 'I':
                inputUnion(S);
                break;
            //相连的机器
            case 'S':
                searchUnion(S,N);
                break;
        }
    }while(in!='S');

}

void initializeUFS(SetType S[],int N){
    for(int i=0;i<N;i++){
        S[i]=-1;
    }
}

void checkUnion(SetType S[]){
    int a=0,b=0;
    ElementType root1=0,root2=0;
    scanf("%d%d",&a,&b);
    //找到两台机器根结点
    root1=Find(S,a-1);/*下标要-1*/
    root2=Find(S,b-1);
    if(root1==root2)
        printf("yes\n");
    else
        printf("no\n");
}

ElementType Find(SetType S[],ElementType node){
    for(;S[node]>=0;node=S[node])
            ;
    return node;
}

void inputUnion(SetType S[]){
    Setname a=0,b=0;
    ElementType root1=0,root2=0;
    scanf("%d%d",&a,&b);
    root1=Find(S,a-1);
    root2=Find(S,b-1);
    if(root1!=root2)
        Union(S,root1,root2);
}

void Union(SetType S[],ElementType root1,ElementType root2){
    /*把root1挂在root2下面*/
    S[root1]=root2;
}

void searchUnion(SetType S[],int N){
    ElementType count=0;
    for(int i=0;i<N;i++){
        if(S[i]==-1) count++;
    }
    if(count==1)
        printf("The network is connected.\n");
    else
        printf("There are %d components.\n",count);
}

测试结果：

之所以会运行超时，原因在于，原代码中

void Union(SetType S[],ElementType root1,ElementType root2){
    /*把root1挂在root2下面*/
    S[root1]=root2;
}

极端情况下会导致树高不断增加，出现下面的情况：

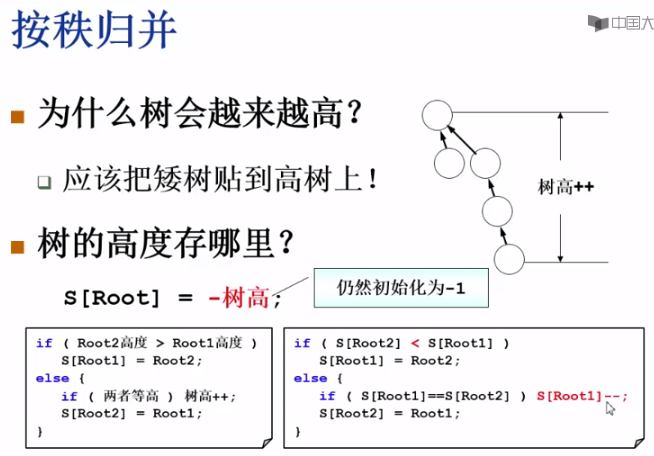
解决方法有两种

• 按秩归并

  • 按树高归并

  

• 按规模归并

  

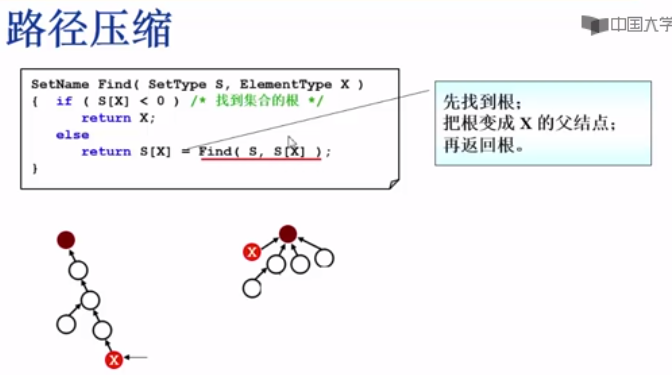
• 路径压缩

  

  最后采用路径压缩：

   #include<stdio.h>
  #include<stdlib.h>
  
  typedef int Setname;
  typedef int ElementType;
  typedef ElementType SetType;/*定义一个elementType数组类型*/
  
  void initializeUFS(SetType S[],int N);
  void checkUnion(SetType S[]);
  ElementType Find(SetType S[],ElementType node);
  void inputUnion(SetType S[]);
  void Union(SetType S[],ElementType root1,ElementType root2);
  void searchUnion(SetType S[],int N);
  
  int main(){
      int N=0;
      char in;
      scanf("%d",&N);
      SetType S[N];
      //初始化
      initializeUFS(S,N);
  
      do{
          scanf("%c",&in);
          switch(in){
              //检查
              case 'C':
                  checkUnion(S);
                  break;
              //连接
              case 'I':
                  inputUnion(S);
                  break;
              //相连的机器
              case 'S':
                  searchUnion(S,N);
                  break;
          }
      }while(in!='S');
  
  }
  
  void initializeUFS(SetType S[],int N){
      for(int i=0;i<N;i++){
          S[i]=-1;
      }
  }
  
  void checkUnion(SetType S[]){
      int a=0,b=0;
      ElementType root1=0,root2=0;
      scanf("%d%d",&a,&b);
      //找到两台机器根结点
      root1=Find(S,a-1);/*下标要-1*/
      root2=Find(S,b-1);
      if(root1==root2)
          printf("yes\n");
      else
          printf("no\n");
  }
  
  ElementType Find(SetType S[],ElementType node){
      /* 一般方法
              1
               \
                2
                 \
                  3
      for(;S[node]>=0;node=S[node])
              ;
      return node;
      */
  
      /* 路径压缩
              1
             / \
            2   3
      */
      if(S[node]<0)
          return node;
      else
          return S[node]=Find(S,S[node]);
  }
  
  void inputUnion(SetType S[]){
      Setname a=0,b=0;
      ElementType root1=0,root2=0;
      scanf("%d%d",&a,&b);
      root1=Find(S,a-1);
      root2=Find(S,b-1);
      if(root1!=root2)
          Union(S,root1,root2);
  }
  
  
  
  
  void Union(SetType S[],ElementType root1,ElementType root2){
      /*  把root1挂在root2下面  */
      S[root1]=root2;
  }
  
  
  
  void searchUnion(SetType S[],int N){
      ElementType count=0;
      for(int i=0;i<N;i++){
          if(S[i]==-1) count++;
      }
      if(count==1)
          printf("The network is connected.\n");
      else
          printf("There are %d components.\n",count);
  }

第六周 图(上)

6.2图的遍历

• 深度优先搜索(deepth search first,DFS)

  类似于先序遍历(递归，所以用到的是系统堆栈)

• 广度优先搜索(breath search first,BFS)

  类似于层次遍历(需要用到辅助queue)

06-图1 列出连通集(25分)

visited数组不要设置为DFS函数的局部变量